一、前端必会算法

郁子大约 31 分钟约 9230 字

（一）数据结构与算法

1.数据结构

可以容纳数据的结构
静态

2.算法

对数据结构进行处理的方法
动态
必须要写严谨性判断，算法程序不允许报错

（二）线性数据结构

又称一维数据结构
强调存储与顺序
几乎没有什么特性

1.数组

申请内存空间由操作系统完成，JS 引擎只能声明需要多大的空间
- 操作系统不一定将扩容的数据存储在原数组末端
- 会直接开辟新的内存空间，先复制原先的数组内容，再在新数组末端存储扩容的数据
- 数组扩容极大地消耗性能

1）特性

存储在物理空间上是连续的
底层的数组长度是不可变的（数组定长）
- 之所以 JS 可以操作数组长度，是因为 JS 引擎作了优化
- 最好在初始化数组时就定好长度
数组的变量 a 指向数组中第一个元素的地址
- a[1] 方括号表示存储地址的偏移

操作系统小知识

通过偏移查询数据的性能最好

2）优点

指定查询某个位置数据的查询性能好

3）缺点

因为空间必须是连续的，所以当数组较大且系统空间碎片较多时，容易存不下
因为数组长度是固定的，所以数组的内容难以被添加和删除

4）声明

数组内容是固定的

const arr = [1, 2, 3, 4, 5];

数组长度是固定的（推荐）

const arr = new Array(10);

2.链表

是一个带有封装属性的结构
链表默认代指单链表
传递一个链表必须传递链表的根节点

警告

每一个节点都认为自己是根节点，即每一个节点都可以当作链表的根节点
因为每一个节点只知道下一个指向的节点，而不知道上一个被指向的节点
因此，要删除链表中某个节点时，只需要把待删除节点的上家指向其下家即可

1）特性

空间上是不连续的
每存放一个值，就会多开辟一块新的引用空间

2）优点

只要内存足够大，就能存得下，无需担心空间碎片的问题
便于添加和删除数据，只需修改前后引用关系的节点

3）缺点

查询某个位置的数据时查询速度慢
每创建一个节点就需要创建一个指向 next 的引用，浪费了一些空间
- 当每一个节点存储的数据越多时，引用浪费的空间影响越小

4）声明

a 和 b 各自存储在不同的物理空间，a 指向 b
此时 a 对象有两个属性
- 属性 1:当前 a 对象存储的值
- 属性 2:a 对象对 b 对象的引用，即存储的是 b 对象的地址

function Node(value) {
  this.value = value;
  this.next = null;
}

let a = new Node(1);
let b = new Node(2);
let c = new Node(3);
let d = new Node(4);

a.next = b;
b.next = c;
c.next = d;
d.next = null;

console.log(a.value); // 1
console.log(a.next.value); // 2
console.log(a.next.next.value); // 3
console.log(a.next.next.next.value); // 4

3.线性数据结构的遍历

遍历：将一个集合中的每一个元素进行获取并查看的操作

1）循环遍历数组

const array = [1, 2, 3, 4, 5, 6, 7, 8, 9];

const searchArray = (arr) => {
  // 算法严谨性要求：必须有严谨性判断，arr.length可能会报错
  if (!arr) return;

  for (let i = 0; i < arr.length; i++) {
    console.log(arr[i]);
  }
};

searchArray(array);

2）循环遍历链表

function Node(val) {
  this.value = val;
  this.next = null;
}
const node1 = new Node(1);
const node2 = new Node(2);
const node3 = new Node(3);
const node4 = new Node(4);
const node5 = new Node(5);
node1.next = node2;
node2.next = node3;
node3.next = node4;
node4.next = node5;

const searchLink = (root) => {
  if (!root) return;
  let node = root;
  while (true) {
    console.log(node.value);
    if (node.next) {
      node = node.next;
    } else {
      break;
    }
    // // 或者
    // if (node) {
    //   console.log(node.value);
    // } else {
    //   break;
    // }
    // node = node.next;
  }
};

searchLink(node1);

3）递归遍历数组

既不推荐，也不常用

const array = [1, 2, 3, 4, 5, 6, 7, 8, 9];

const searchArray = (arr, i) => {
  if (!arr || i >= arr.length) return;
  console.log(arr[i]);
  searchArray(arr, i + 1);
};

searchArray(array, 0);

4）递归遍历链表

性能没有循环遍历好
链表通常使用递归遍历

function Node(val) {
  this.value = val;
  this.next = null;
}
const node1 = new Node(1);
const node2 = new Node(2);
const node3 = new Node(3);
const node4 = new Node(4);
const node5 = new Node(5);
node1.next = node2;
node2.next = node3;
node3.next = node4;
node4.next = node5;

const searchLink = (root) => {
  if (!root) return;
  console.log(root.value);
  searchLink(root.next);
};

searchLink(node1);

警告

递归必须有出口，即 return 的时间点

4.链表的逆置

关键点在于找到最后一个节点
因为最后一个节点的 next 指向 null
最后一个节点指向倒数第二个节点，再依次指回第一个节点
原先的根节点在逆置后必须指向 null，否则前面两个节点互指，陷入循环

1）找到最后一个节点

不可行
即使当前 node5 的 next 指向 null，它也不会认为自己是最后一个节点
会认为自己是一个链表的根节点，但是链表只有一个节点

const findLastNode = (root) => {
  return root.next ? findLastNode(root.next) : root;
};
console.log(findLastNode(node1));
// Node { value: 5, next: null }

2）找到倒数第二个节点

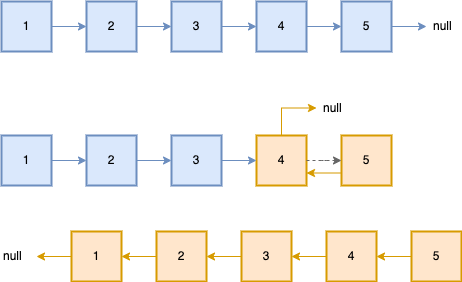
// 逆置前
const searchLink = (root) => {
  if (!root) return;
  console.log(root.value);
  searchLink(root.next);
};
searchLink(node1); // 1 2 3 4 5

// 逆置
const reverseLink = (root) => {
  if (!root.next.next) {
    // 当前是倒数第二个节点（node4）

    // 最后一个节点（node5）的next指向当前节点（node4）
    root.next.next = root;

    // 返回逆置后的根节点（node5）【递归出口】
    return root.next;
  } else {
    // 当前root位置在倒数第二个之前

    // 保存递归逆置后的根节点（node5）
    const newRoot = reverseLink(root.next);

    // 位置靠前的节点都要让下一个节点指向自己，同时自己的next置空（才能消除node1和node2互指的循环）
    root.next.next = root;
    root.next = null;

    // 将逆置后的根节点（node5）返还给上一级递归保存
    return newRoot;
  }
};

// 逆置后
searchLink(reverseLink(node1)); // 5 4 3 2 1

（三）排序

排序不是比较大小
- 比较的可能是其他属性
本质是比较和交换
- 根据比较的结果判断是否需要交换

注意

任何一种排序算法都没有优劣之分，只有是否适合的场景
数组越有序越适合冒泡排序，性能最好
选择排序性能居中
数组越乱序越适合快速排序

1.比较

排序的结果由比较函数确定
Array.prototype.sort 传递的参数其实就是比较函数

// 比较后得出是否需要交换当前a和b
const compare = (a, b) => a - b < 0;

2.交换

交换数组中的两个值

// 将数组中的a和b位置上的值交换
const exchange = (arr, a, b) => {
  let temp = arr[a];
  arr[a] = arr[b];
  arr[b] = temp;
};

3.冒泡排序

每一次循环都会把数组中第一个满足比较函数的值排到末端

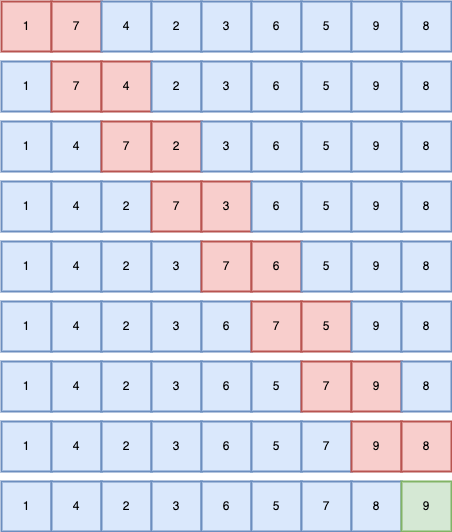
const array = [1, 7, 4, 2, 3, 6, 5, 9, 8];

// sort函数可以是冒泡排序、选择排序或其他任何排序算法
const sort = (arr) => {
  // 数组中的每一位都要经历一趟排序
  for (let i = 0; i < arr.length; i++) {
    // -i 表示下一趟排序时不用再比较倒数第二位和最后一位数
    // -1 是为了防止 j + 1 溢出
    for (let j = 0; j < arr.length - 1 - i; j++) {
      if (compare(arr[j], arr[j + 1])) {
        exchange(arr, j, j + 1);
      }
    }
  }
};

sort(array);
console.log(array); // [1, 2, 3, 4, 5, 6, 7, 8, 9]

4.选择排序

内层每一趟循环选出满足比较函数的最大下标的值排到数组末端
冒泡排序是找到一个需要排序的值就立马交换
选择排序是全部遍历一遍后找到最后一个需要排序的值再交换

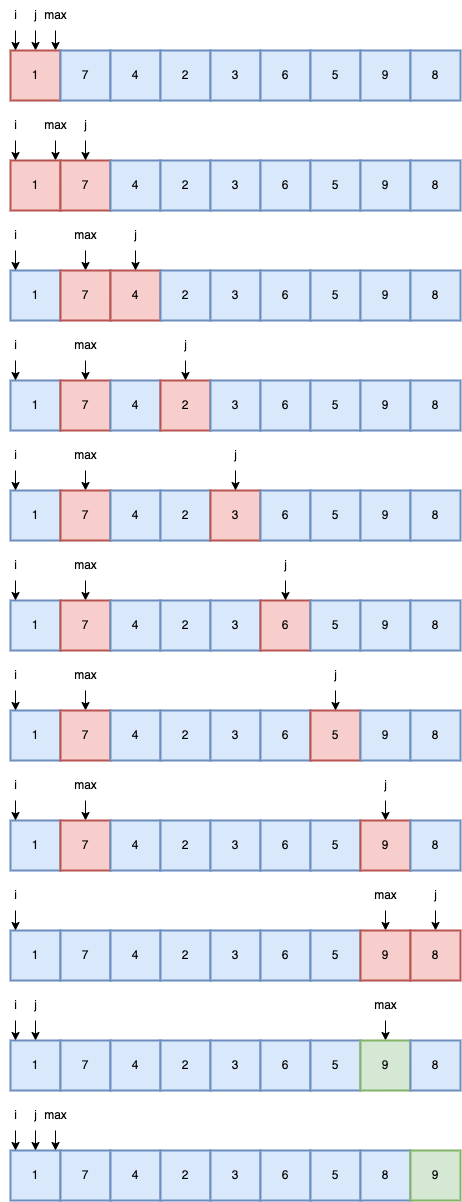
const array = [1, 7, 4, 2, 3, 6, 5, 9, 8];

// sort函数可以是冒泡排序、选择排序或其他任何排序算法
const sort = (arr) => {
  // 数组中每一位都要经历一趟排序
  for (let i = 0; i < arr.length; i++) {
    // -i 表示下一趟排序时不用再比较前面几趟排好的值
    let maxIndex = 0;
    for (let j = 0; j < arr.length - i; j++) {
      if (compare(arr[j], arr[maxIndex])) {
        maxIndex = j;
      }
    }
    // 交换最后一位满足的值 和 内层循环最后一个数（最后一个没有排过序的值）
    exchange(arr, arr.length - i - 1, maxIndex);
  }
};

sort(array);
console.log(array); // [1, 2, 3, 4, 5, 6, 7, 8, 9]

5.简单快速排序

1）思想

选定某个元素为基准元素
遍历数组，比基准元素小的排前，比基准元素大的排后
递归排序左右的数组
最后合并输出

2）排序

创建了许多数组，牺牲了性能
比完整版更容易理解

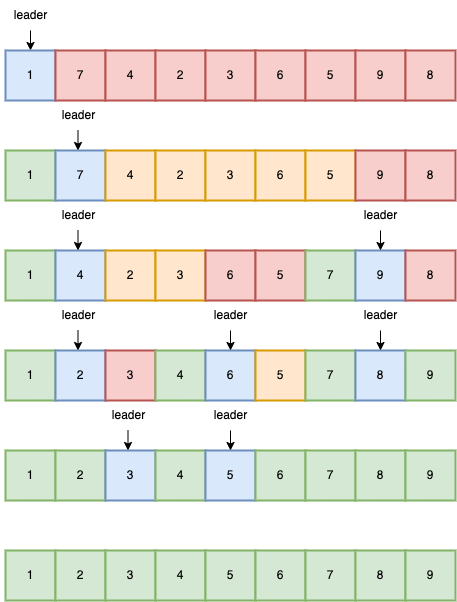
const array = [1, 7, 4, 2, 3, 6, 5, 9, 8];

// sort函数可以是冒泡排序、选择排序或其他任何排序算法
const sort = (arr) => {
  // 严谨性判断
  if (!arr || arr.length === 0) return [];

  // 选定基准元素
  const leader = arr[0];

  // 遍历排序左右数组
  let left = [],
    right = [];
  for (let i = 1; i < arr.length; i++) {
    if (compare(leader, arr[i])) left.push(arr[i]);
    else right.push(arr[i]);
  }
  console.log(left, leader, right);

  // 递归排序左右数组
  return [...sort(left), leader, ...sort(right)];
};

console.log(sort(array)); // [1, 2, 3, 4, 5, 6, 7, 8, 9]

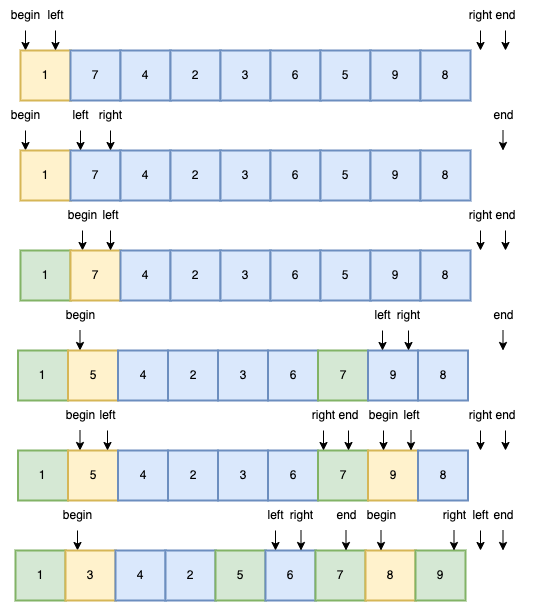
6.标准快速排序

1）思想

选定某个基准元素
设定左右指针遍历剩余元素，分为左右两个区间
左右指针相遇后交换基准元素和右指针
- 相遇时 left === right
  - 说明当前左指针的上一位的值满足比较函数
  - 且当前左指针指向的值不满足比较函数
  - 应该交换基准元素和当前左/右指针的上一位
- 相遇时 left === right + 1
  - 说明当前右指针指向的值满足比较函数
    - 所以左指针会指向下一位
  - 应该交换基准元素和当前右指针指向的元素
递归排序左右区间

警告

程序中涉及到区间通常都是左闭右开区间

2）排序

const array = [1, 7, 4, 2, 3, 6, 5, 9, 8];

// sort函数可以是冒泡排序、选择排序或其他任何排序算法
const sort = (arr) => {
  const quickSort = (arr, begin, end) => {
    // 严谨性判断
    if (begin >= end - 1) return;

    // 声明左右指针
    let left = begin,
      right = end;

    // 选定begin为基准元素划分左右区间
    do {
      // 判断条件前会先执行一次，实际上left是从begin+1开始
      do {
        left++;
      } while (left < right && arr[left] < arr[begin]);
      do {
        right--;
      } while (left < right && arr[right] >= arr[begin]);
      if (left < right) exchange(arr, left, right);
    } while (left < right);

    // 保存基准元素交换点
    const swapTemp = left === right ? right - 1 : right;

    // 交换基准元素
    exchange(arr, begin, swapTemp);

    // 递归排序左右区间
    quickSort(arr, begin, swapTemp);
    quickSort(arr, swapTemp + 1, end);
  };
  quickSort(arr, 0, arr.length);
};

sort(array);
console.log(array); // [1, 2, 3, 4, 5, 6, 7, 8, 9]

（四）栈和队列

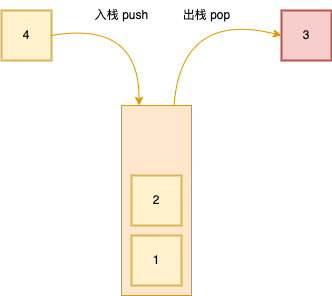
1.栈结构

先进后出
类比纸箱
JS 实现极其简单，得益于数组底层封装为动态数组
- 可调节长度，且有 push 和 pop 方法

function Stack() {
  this.arr = [];

  this.push = (value) => {
    this.arr.push(value);
  };

  this.pop = () => {
    return this.arr.pop();
  };
}

const stack = new Stack();

stack.push(1);
stack.push(2);
stack.push(3);
console.log(stack.arr); // [ 1, 2, 3 ]

stack.pop();
console.log(stack.arr); // [ 1, 2 ]

stack.pop();
console.log(stack.arr); // [ 1 ]

stack.pop();
console.log(stack.arr); // []

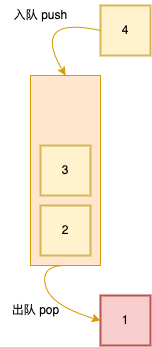
2.队列结构

先进先出
类比管道
JS 实现极其简单，得益于数组底层封装为动态数组
- 可调节长度，且有 shift 和 unshift 方法

function Queue() {
  this.arr = [];

  this.push = (value) => {
    this.arr.push(value);
  };

  this.pop = () => {
    return this.arr.shift();
  };
}

const queue = new Queue();

queue.push(1);
queue.push(2);
queue.push(3);
console.log(queue.arr); // [ 1, 2, 3 ]

queue.pop();
console.log(queue.arr); // [ 2, 3 ]

queue.pop();
console.log(queue.arr); // [ 3 ]

queue.pop();
console.log(queue.arr); // []

（五）双向链表

1.优点

无论给出哪一个节点，都可以遍历整个链表

2.缺点

比单链表多耗费一个引用的空间
构建双链表比单链表复杂
双链表能实现的操作单链表都能实现

3.实现

function Node(val) {
  this.value = val;
  this.next = null;
  this.prev = null;
}
const node1 = new Node(1);
const node2 = new Node(2);
const node3 = new Node(3);
const node4 = new Node(4);
const node5 = new Node(5);

node1.next = node2;
node2.prev = node1;
node2.next = node3;
node3.prev = node2;
node3.next = node4;
node4.prev = node3;
node4.next = node5;
node5.prev = node4;

（六）二维数据结构

1.二维拓扑结构（图）

1）拓扑

只看对象之间的关系是否相同
不关注其大小、方向、位置等是否相同

2）二维

只要研究的对象之间有关系，都可以映射到二维平面上研究

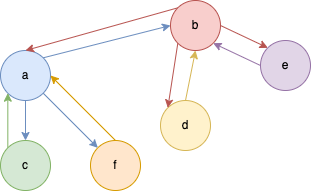
3）实现

二维数组由一位数组衍生而来
图由链表衍生而来
关系是双向的

function Node(val) {
  this.value = val;
  this.neighbor = [];
}
const a = new Node("a");
const b = new Node("b");
const c = new Node("c");
const d = new Node("d");
const e = new Node("e");
const f = new Node("f");

a.neighbor.push(b);
a.neighbor.push(c);
a.neighbor.push(f);

b.neighbor.push(a);
b.neighbor.push(d);
b.neighbor.push(e);

c.neighbor.push(a);

d.neighbor.push(b);

e.neighbor.push(b);

f.neighbor.push(a);

2.邻接表

（七）树形结构

特殊的拓扑结构
又称为有向无环图

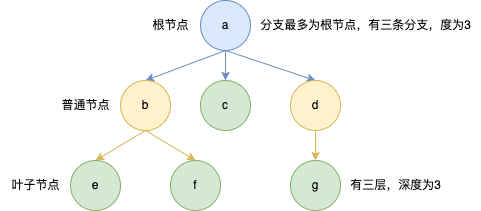
1.基本特点

永远不可能形成回路
只有一个根节点

概念	含义
叶子节点	没有指向任何节点的节点
普通节点	既不是根节点也不是叶子节点的节点
度	分支最多的节点的分支数
深度	根节点到最远的叶子节点的层数

2.二叉树

度为 2 的树结构

1）满二叉树

所有叶子节点都在树的最底层
每个非叶子节点都有两个子节点

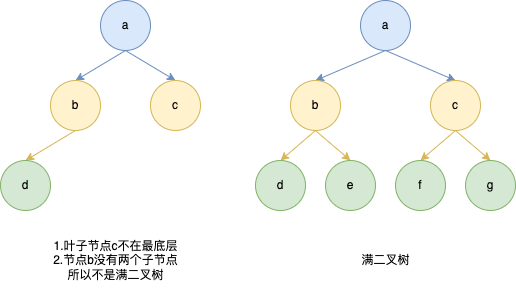
2）完全二叉树（国内定义）

所有叶子节点都在树的最后一层或倒数第二层
所有叶子节点都向左聚拢

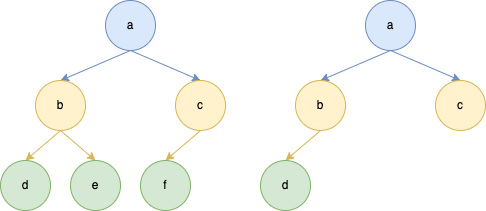
3）完全二叉树（国际定义）

所有叶子节点都在树的最后一层或倒数第二层
如果有叶子节点，就必须有两个叶子节点

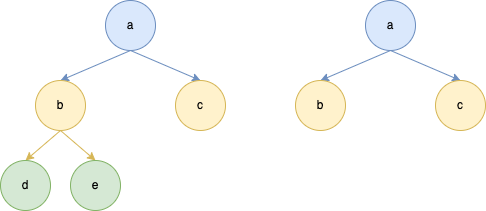
4）子树

在二叉树中，所有节点都认为自己是根节点
子树：在二叉树中，每一个节点或叶子节点，都是一颗子树的根节点

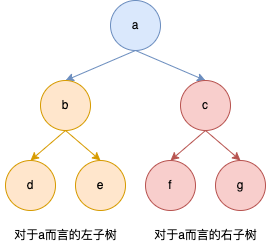
3.二叉树的遍历

传递二叉树要传根节点

分类	含义
前序遍历/先根次序遍历	根-左-右
中序遍历/中根次序遍历	左-根-右
后序遍历/后根次序遍历	左-右-根

提示

对于简单二叉树，中序遍历可以理解为每个节点在树的底部 x 轴上的投影从左到右的顺序

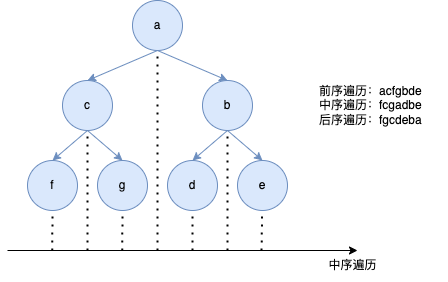
1）构造树

function Node(val) {
  this.value = val;
  this.left = null;
  this.right = null;
}
const a = new Node("a");
const b = new Node("b");
const c = new Node("c");
const d = new Node("d");
const e = new Node("e");
const f = new Node("f");
const g = new Node("g");

a.left = c;
a.right = b;
c.left = f;
c.right = g;
b.left = d;
b.right = e;

2）前序遍历

let res = "";
const firstSearch = (root) => {
  if (!root) return;
  res += root.value;
  firstSearch(root.left);
  firstSearch(root.right);
  return res;
};
console.log(firstSearch(a)); // acfgbde

3）中序遍历

let res = "";
const centerSearch = (root) => {
  if (!root) return;
  centerSearch(root.left);
  res += root.value;
  centerSearch(root.right);
  return res;
};
console.log(centerSearch(a)); // fcgadbe

4）后序遍历

let res = "";
const lastSearch = (root) => {
  if (!root) return;
  lastSearch(root.left);
  lastSearch(root.right);
  res += root.value;
  return res;
};
console.log(lastSearch(a)); // fgcdeba

4.还原二叉树

还原二叉树必须给出中序遍历

1）根据前序中序还原二叉树

function Node(val) {
  this.value = val;
  this.left = null;
  this.right = null;
}

// 根据前序中序还原二叉树
const first = ["a", "c", "f", "g", "b", "d", "e"];
const center = ["f", "c", "g", "a", "d", "b", "e"];
const getTreeFromFirstAndCenter = (first, center) => {
  if (!first || !center || first.length === 0 || center.length === 0 || first.length !== center.length) return null;

  const root = new Node(first[0]);

  // 找出中序遍历中根节点的下标
  const rootIndex = center.indexOf(root.value);

  // 划分前序和中序中的左右子树区间
  const firstLeft = first.slice(1, rootIndex + 1);
  const firstRight = first.slice(rootIndex + 1, first.length);
  const centerLeft = center.slice(0, rootIndex);
  const centerRight = center.slice(rootIndex + 1, center.length);

  // 递归生成左右子树
  root.left = getTreeFromFirstAndCenter(firstLeft, centerLeft);
  root.right = getTreeFromFirstAndCenter(firstRight, centerRight);
  return root;
};
console.log(getTreeFromFirstAndCenter(first, center));

2）根据中序后序还原二叉树

function Node(val) {
  this.value = val;
  this.left = null;
  this.right = null;
}

// 根据中序后序还原二叉树
const center = ["f", "c", "g", "a", "d", "b", "e"];
const last = ["f", "g", "c", "d", "e", "b", "a"];
const getTreeFromCenterAndLast = (center, last) => {
  if (!center || !last || center.length === 0 || last.length === 0 || last.length !== center.length) return null;

  const root = new Node(last[last.length - 1]);

  // 找出中序遍历中根节点的下标
  const rootIndex = center.indexOf(root.value);

  // 划分中序和后序中的左右子树区间
  const centerLeft = center.slice(0, rootIndex);
  const centerRight = center.slice(rootIndex + 1, center.length);
  const lastLeft = last.slice(0, rootIndex);
  const lastRight = last.slice(rootIndex, last.length - 1);

  // 递归生成左右子树
  root.left = getTreeFromCenterAndLast(centerLeft, lastLeft);
  root.right = getTreeFromCenterAndLast(centerRight, lastRight);
  return root;
};
console.log(getTreeFromCenterAndLast(center, last));

（八）搜索

树的搜索
图的搜索
爬虫的逻辑
搜索引擎的爬虫算法

1.二叉树的搜索

1）深度优先搜索

只要有子节点就继续查找子节点
- 没有子节点再继续往上找未遍历的兄弟节点
能往下就往下，适合探索未知
对于二叉树来说，深度优先搜索的节点遍历顺序，和前序遍历的顺序是一样的

const deepSearch = (root, target) => {
  if (!root) return false;
  // console.log(root.value); // a c f g b d e
  if (root.value === target) return true;
  return deepSearch(root.left, target) || deepSearch(root.right, target);
};
console.log(deepSearch(a, "f")); // true
console.log(deepSearch(a, "n")); // false

2）广度优先搜索

只要有兄弟节点就继续查找兄弟节点
- 没有兄弟节点再继续找之前第一个兄弟节点未遍历的子节点
一层一层往下找，适合探索局域
遍历每一个节点时，将其子节点存入数组中，即获得下一层需要遍历的节点

const breadthSearch = (rootList, target) => {
  if (!rootList || rootList.length === 0) return false;
  const children = [];
  for (let i = 0; i < rootList.length; i++) {
    if (rootList[i]) {
      // console.log(rootList[i].value); // a c b f g d e
      if (rootList[i].value === target) return true;
      children.push(rootList[i].left);
      children.push(rootList[i].right);
    }
  }
  return breadthSearch(children, target);
};
console.log(breadthSearch([a], "f")); // true
console.log(breadthSearch([a], "n")); // false

2.二叉树的比较

必须明确两个点
- 两棵树都为空时是否相同
- 左右子树互换位置后是否相同
面试时尽量问一下
笔试时如果没有明确说明“左右子树互换后仍视为同一棵树”，则默认互换后不是同一棵树

1）左右子树互换后不是同一棵树

const compareTree = (root1, root2) => {
  // 都为空或结构相同
  if ((!root1 && !root2) || root1 === root2) return true;

  // 一棵为空另一棵不为空
  if ((!root1 && root2) || (root1 && !root2)) return false;

  // 相同位置的节点的值不同
  if (root1.value !== root2.value) return false;

  // 左右子树分别相同时才相同
  return compareTree(root1.left, root2.left) && compareTree(root1.right, root2.right);
};
console.log(compareTree(a1, a2)); // true

2）左右子树互换后视为同一棵树

const compareTree = (root1, root2) => {
  // 都为空或结构相同
  if ((!root1 && !root2) || root1 === root2) return true;

  // 一棵为空另一棵不为空
  if ((!root1 && root2) || (root1 && !root2)) return false;

  // 相同位置的节点的值不同
  if (root1.value !== root2.value) return false;

  // 左右子树分别相同或镜像相同时才相同
  return (
    (compareTree(root1.left, root2.left) && compareTree(root1.right, root2.right)) ||
    (compareTree(root1.left, root2.left) && compareTree(root1.right, root2.right))
  );
};
console.log(compareTree(a1, a2)); // true

3.二叉树的 diff 算法

在比较的过程中得到新增、修改、删除的节点信息

{
  diffList: [{
    type: 'Add',
    origin: null,
    now: c2
  }, {
    type: 'Edit',
    origin: b1,
    now: b2
  }, {
    type: 'Delete',
    origin: n,
    now: null
  }]
}

如果当前比较的节点被修改了，必须再次 diff
当前节点修改了不代表其子节点也被修改了

const diffTree = (root1, root2, diffList) => {
  if (root1 === root2) return diffList;
  if (!root1 && root2) {
    // 新增
    diffList.push({
      type: "Add",
      origin: null,
      new: root2,
    });
  } else if (root1 && !root2) {
    // 删除
    diffList.push({
      type: "Delete",
      origin: root1,
      new: null,
    });
  } else if (root1.value !== root2.value) {
    // 修改
    diffList.push({
      type: "Edit",
      origin: root1,
      new: root2,
    });
    diffTree(root1.left, root2.left, diffList);
    diffTree(root1.right, root2.right, diffList);
  } else {
    diffTree(root1.left, root2.left, diffList);
    diffTree(root1.right, root2.right, diffList);
  }
  return diffList;
};
const diffList = [];
diffTree(a1, a2, diffList);
console.log(diffList);

4.图的搜索（最小生成树问题）

1）目标

希望所有节点都连通，所需花费（副作用）最少
由于树又叫有向无环图，该问题需要的就是无环图，所以称为最小生成树

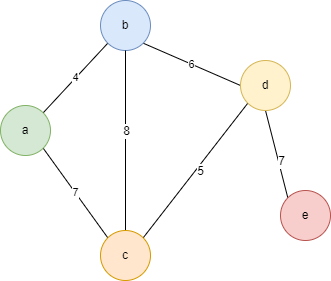
2）图的表示

表示一个图，可以使用点集合和边集合
映射为二维数组的表格形式

	A	B	C	D	E
A	0	4	7	Max	Max
B	4	0	8	6	Max
C	7	8	0	5	Max
D	Max	6	5	0	7
E	Max	Max	Max	7	0

const MAX = 1000000;

function Node(val) {
  this.value = val;
  this.neighbors = [];
}

// 点集合
const POINTS = ["A", "B", "C", "D", "E"].map((p) => new Node(p));

// 边集合
const DISTANCE = [
  [0, 4, 7, MAX, MAX],
  [4, 0, 8, 6, MAX],
  [7, 8, 0, 5, MAX],
  [MAX, 6, 5, 0, 7],
  [MAX, MAX, MAX, 7, 0],
];

3）算法 1：普利姆算法（加点法）

任选一个节点作为起点
找到以当前节点为起点且路径最短的边
如果这条边的另一个节点没有被连通，则将该节点连接
如果这条边的另一个节点已经被连通，则继续找路径倒数第二短的边
重复步骤 2-4 直到将所有节点连通为止

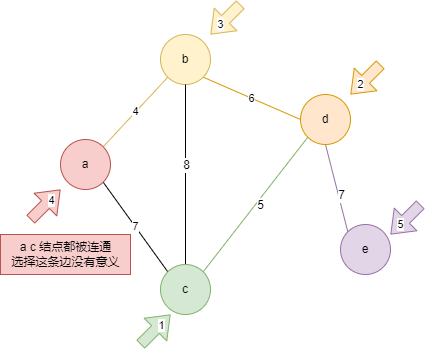
const connected = [];

// 根据当前节点在点集中的下标，找到其在边集中的下标
const getNodeIndexInPoints = (val) => {
  for (let i = 0; i < POINTS.length; i++) {
    if (POINTS[i].value === val) return i;
  }
  return -1;
};

// 遍历已连接的点集，找到以每个节点为起点且路径最短的边
const getMinDistanceNode = (points, distance, connected) => {
  let startNode = null,
    nextNode = null,
    min = MAX;
  for (let i = 0; i < connected.length; i++) {
    const row = distance[getNodeIndexInPoints(connected[i].value)];
    for (let j = 0; j < row.length; j++) {
      // 不是当前点本身，与当前点之间有通路，没有被连接过的点才能继续比较距离长短
      if (row[j] === 0 || row[j] === MAX || connected.includes(points[j])) continue;

      if (row[j] < min) {
        startNode = connected[i];
        nextNode = points[j];
        min = row[j];
      }
    }
  }
  // 连接起点和最短边端点
  startNode.neighbors.push(nextNode);
  nextNode.neighbors.push(startNode);
  return nextNode;
};

const prim = (points, distance, start) => {
  connected.push(start);
  // 获取最小代价的边
  while (true) {
    // 所有的节点都连通了
    if (connected.length === points.length) break;

    const minDistanceNode = getMinDistanceNode(points, distance, connected);
    connected.push(minDistanceNode);
  }
};
prim(POINTS, DISTANCE, POINTS[2]);
console.log(connected);

/* 
[
  Node { value: 'C', neighbors: [ [Node] ] },
  Node { value: 'D', neighbors: [ [Node], [Node], [Node] ] },
  Node { value: 'B', neighbors: [ [Node], [Node] ] },
  Node { value: 'A', neighbors: [ [Node] ] },
  Node { value: 'E', neighbors: [ [Node] ] }
]
 */

4）算法 2：克鲁斯卡尔算法（加边法）

选择路径最短的边，连接左右两端的节点，形成一个组
要保证连接的两端的节点至少有一个点是未连接的节点
如果两端的节点都被连接过，那么要保证两端的节点都属于两个组
重复步骤 1-3 直到将所有节点连通为止

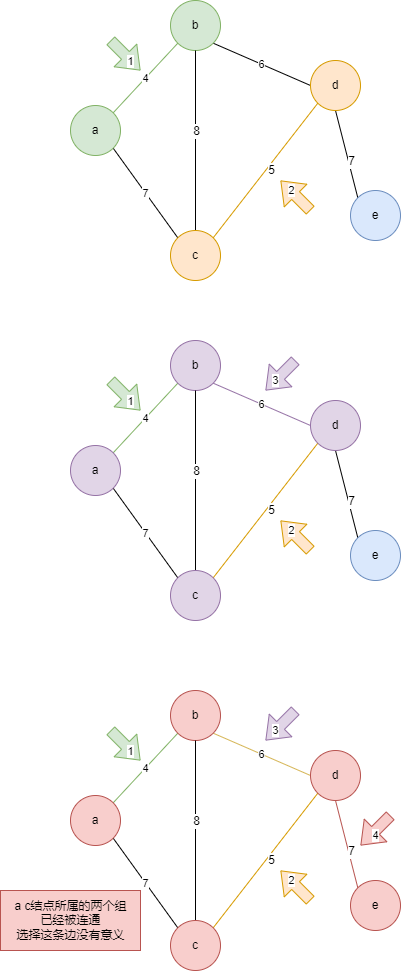
// 二维数组，每一个子数组表示图上已连接的组
const connected = [];

// 获取节点在已连接的集合中所属的组
const getGroupInConnected = (node) => {
  for (let i = 0; i < connected.length; i++) {
    if (connected[i].includes(node)) {
      return connected[i];
    }
  }
  return null;
};

// 判断当前两个点是否满足连接的要求
const judgeConnect = (node1, node2) => {
  /**
   * 1.两个点都未连接（不属于任何组）=> 可以连接，产生一个新的组
   * 2.点1在A组，点2未连接 => 可以连接，点2加入A组
   * 3.点1未连接，点2在B组 => 可以连接，点1加入B组
   * 4.点1在A组，点2在B组 => 可以连接，合并两个组产生一个新的组，移除原先的两个组
   * 5.点1和点2在同一个组 => 不可以连接
   */
  groupA = getGroupInConnected(node1);
  groupB = getGroupInConnected(node2);
  if (groupA && groupB && groupA === groupB) return false;
  return true;
};

// 连接最短路径的左右端点
const handleConnectNode = (node1, node2) => {
  /**
   * 1.两个点都未连接（不属于任何组）=> 可以连接，产生一个新的组
   * 2.点1在A组，点2未连接 => 可以连接，点2加入A组
   * 3.点1未连接，点2在B组 => 可以连接，点1加入B组
   * 4.点1在A组，点2在B组 => 可以连接，合并两个组产生一个新的组，移除原先的两个组
   */
  groupA = getGroupInConnected(node1);
  groupB = getGroupInConnected(node2);
  if (!groupA && !groupB) {
    connected.push([node1, node2]);
  } else if (groupA && !groupB) {
    groupA.push(node2);
  } else if (!groupA && groupB) {
    groupB.push(node1);
  } else if (groupA && groupB && groupA !== groupB) {
    connected.push([...groupA, ...groupB]);

    // A、B组查找到后就立即删除，否则B组先找到的下标在A组被删掉后会变化
    const groupAIndex = connected.indexOf(groupA);
    connected.splice(groupAIndex, 1);
    const groupBIndex = connected.indexOf(groupB);
    connected.splice(groupBIndex, 1);
  }
  node1.neighbors.push(node2);
  node2.neighbors.push(node1);
};

const kruskal = (points, distance) => {
  while (true) {
    if (connected.length === 1 && connected[0].length === POINTS.length) break;

    let startNode = null,
      nextNode = null,
      min = MAX;
    for (let i = 0; i < distance.length; i++) {
      for (let j = 0; j < distance[i].length; j++) {
        const dis = distance[i][j];

        // 不是当前点本身，与当前点之间有通路，距离比当前已找到的最短路径还短才能连接
        if (dis === 0 || dis === MAX) continue;

        if (dis < min && judgeConnect(points[i], points[j])) {
          startNode = points[i];
          nextNode = points[j];
          min = dis;
        }
      }
    }
    handleConnectNode(startNode, nextNode);
  }
};

kruskal(POINTS, DISTANCE);
console.log(connected);

/* 
[
  [
    Node { value: 'A', neighbors: [Array] },
    Node { value: 'B', neighbors: [Array] },
    Node { value: 'C', neighbors: [Array] },
    Node { value: 'D', neighbors: [Array] },
    Node { value: 'E', neighbors: [Array] }
  ]
]
 */

5.二叉搜索树

1）经典问题

有一万个数字，写一个方法查找给定的数，返回存在或不存在
要求性能尽可能的好

const arr = [];
for (let i = 0; i < 10000; i++) {
  arr[i] = Math.floor(Math.random() * 10000);
}

/**
 * 用数组实现
 */
let count = 0;
const normalSearch = (arr, target) => {
  for (let i = 0; i < arr.length; i++) {
    count++;
    if (arr[i] === target) return true;
  }
  return false;
};
console.log(normalSearch(arr, 1000), count); // true 3394

2）构建二叉搜索树

二叉搜索树，又叫二叉排序树
左子树的节点都比根节点小，右子树的节点都比根节点大

function Node(val) {
  this.value = val;
  this.left = null;
  this.right = null;
}

// 添加节点
const addNode = (root, val) => {
  if (!root || root.value === val) return;
  if (root.value < val) {
    if (!root.right) root.right = new Node(val);
    else addNode(root.right, val);
  } else {
    if (!root.left) root.left = new Node(val);
    else addNode(root.left, val);
  }
};

// 构建二叉搜索树
const buildSearchTree = (arr) => {
  if (!arr || arr.length === 0) return;
  const root = new Node(arr[0]);
  for (let i = 1; i < arr.length; i++) {
    addNode(root, arr[i]);
  }
  return root;
};

3）搜索二叉搜索树

/**
 * 用二叉搜索树实现
 */
let count2 = 0;
const searchBySearchTree = (root, target) => {
  if (!root) return false;
  count2++;
  if (root.value === target) return true;
  else if (root.value < target) return searchBySearchTree(root.right, target);
  else return searchBySearchTree(root.left, target);
};

const root = buildSearchTree(arr);
console.log(searchBySearchTree(root, 1000), count2); // true 11

二叉搜索树缺点

选取的根节点排序靠前或靠后时，搜索时每一层节点数不多，但是层数较多

6.平衡二叉树（二叉平衡搜索树）

根节点的左子树和右子树的高度差不超过 1
每棵子树都应该满足第一点

// 获取树的深度
const getDeep = (root) => {
  if (!root) return 0;
  return Math.max(getDeep(root.left), getDeep(root.right)) + 1;
};

// 判断是否是平衡二叉树
const isBalanceTree = (root) => {
  if (!root) return true;
  if (Math.abs(getDeep(root.left) - getDeep(root.right)) > 1) return false;
  return isBalanceTree(root.left) && isBalanceTree(root.right);
};
console.log(isBalanceTree(a));

7.二叉树的单旋

作用：将不平衡的二叉树转换为平衡二叉树
分为左单旋、右单旋
某一节点不平衡
- 如果左边浅，右边深，则进行左单旋操作
- 如果左边深，右边浅，则进行右单旋操作

概念	含义
旋转节点	不平衡的节点
新根	旋转后成为根节点的节点
变化分支	父节点发生变化的分支
不变分支	父节点没有变化的分支

提示

对不平衡二叉树操作要按照后序遍历的顺序找旋转节点
即从下层节点开始操作
因为有可能子树平衡后，父节点也平衡了

1）左单旋

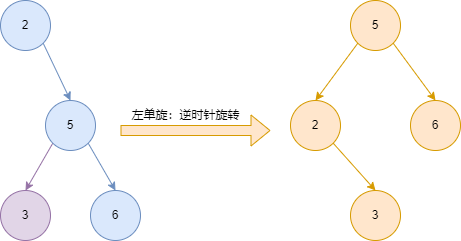
概念	含义	图中节点
旋转节点	当前不平衡的节点	2
新根	右子树的根节点	5
变化分支	旋转节点的右子树的左子树	3
不变分支	旋转节点的右子树的右子树	6

找到新根
找到变化分支
当前旋转节点的右子树节点为变化分支
新根的左子树节点为旋转节点
返回新的根节点

const handleLeftRotate = (root) => {
  // 找到新根
  let newRoot = root.right;
  // 找到变化分支
  let changeBranch = root.right.left;
  // 当前旋转节点的右子树节点为变化分支
  root.right = changeBranch;
  // 新根的左子树节点为旋转节点
  newRoot.left = root;
  // 返回新的根节点
  return newRoot;
};

2）右单旋

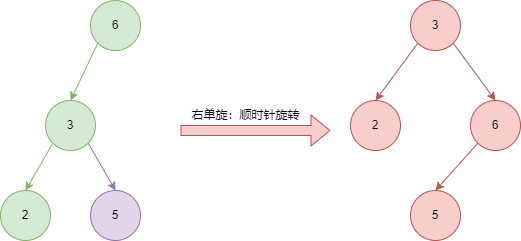
概念	含义	图中节点
旋转节点	当前不平衡的节点	6
新根	左子树的根节点	3
变化分支	旋转节点的左子树的右子树	5
不变分支	旋转节点的左子树的左子树	2

找到新根
找到变化分支
当前旋转节点的左子树节点为变化分支
新根的右子树节点为旋转节点
返回新的根节点

const handleRightRotate = (root) => {
  // 找到新根
  let newRoot = root.left;
  // 找到变化分支
  let changeBranch = root.left.right;
  // 当前旋转节点的左子树节点为变化分支
  root.left = changeBranch;
  // 新根的右子树节点为旋转节点
  newRoot.right = root;
  // 返回新的根节点
  return newRoot;
};

3）转换不平衡二叉树

const handleChangeToBalanceTree = (root) => {
  if (isBalanceTree(root)) return root;

  if (!root.left) root.left = handleChangeToBalanceTree(root.left);
  if (!root.right) root.right = handleChangeToBalanceTree(root.right);

  const leftDeep = getDeep(root.left),
    rightDeep = getDeep(root.right);
  if (Math.abs(leftDeep - rightDeep) < 2) {
    return true;
  } else if (leftDeep > rightDeep) {
    // 左边深，右旋
    return handleRightRotate(root);
  } else {
    // 右边深，左旋
    return handleLeftRotate(root);
  }
};

console.log(isBalanceTree(node2)); // false
const newRoot = handleChangeToBalanceTree(node2);
console.log(isBalanceTree(newRoot)); // true

8.二叉树的双旋

1）单旋解决不了的情况

变化分支(7-6)不可以是唯一的最深分支

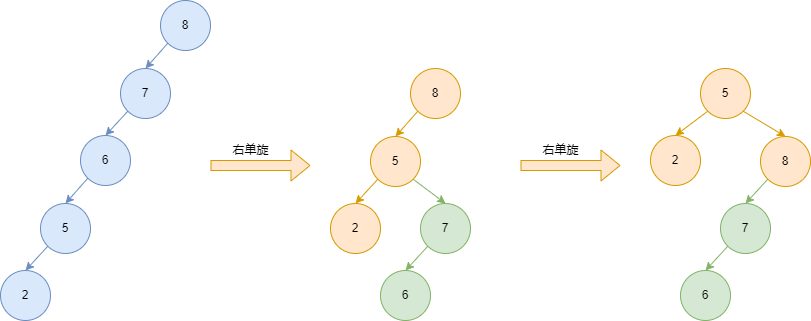
需要先反向旋转变化分支（左右双旋）

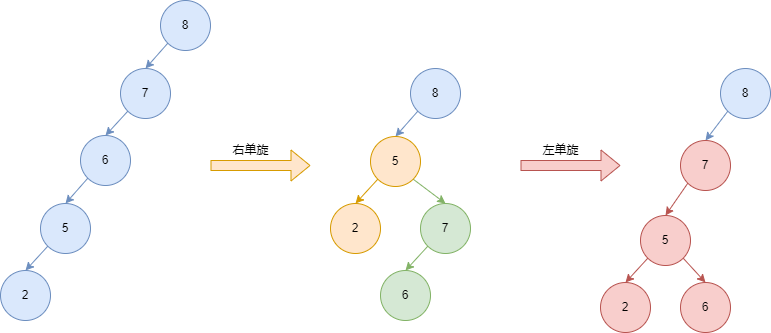
2）左右双旋

当要对某个节点进行右单旋时，如果变化分支是唯一的最深分支
则要对新根进行左单旋
再进行右单旋

3）右左双旋

当要对某个节点进行左单旋时，如果变化分支是唯一的最深分支
则要对新根进行右单旋
再进行左单旋

4）左右双旋和右左双旋代码实现

const handleChangeToBalanceTree = (root) => {
  if (isBalanceTree(root)) return root;

  if (!root.left) root.left = handleChangeToBalanceTree(root.left);
  if (!root.right) root.right = handleChangeToBalanceTree(root.right);

  const leftDeep = getDeep(root.left),
    rightDeep = getDeep(root.right);
  if (Math.abs(leftDeep - rightDeep) < 2) {
    return root;
  } else if (leftDeep > rightDeep) {
    // 左边深
    // 判断是否需要右左双旋
    const changeBranchDeep = getDeep(root.left.right);
    const noChangeBranchDeep = getDeep(root.left.left);
    if (changeBranchDeep > noChangeBranchDeep) {
      root.left = handleLeftRotate(root.left);
    }
    // 右旋
    return handleRightRotate(root);
  } else {
    // 右边深
    // 判断是否需要左右双旋
    const changeBranchDeep = getDeep(root.right.left);
    const noChangeBranchDeep = getDeep(root.right.right);
    if (changeBranchDeep > noChangeBranchDeep) {
      root.right = handleRightRotate(root.right);
    }
    // 左旋
    return handleLeftRotate(root);
  }
};

4）左右双旋和右左双旋解决不了的情况

变化分支不是唯一的最深分支
但是变化分支的高度和旋转节点另一侧的高度差距超过 2
则单旋之后依旧不平衡

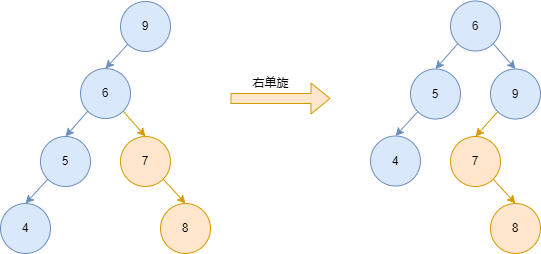
5）左左双旋和右右双旋的代码实现

const handleChangeToBalanceTree = (root) => {
  if (isBalanceTree(root)) return root;

  if (!root.left) root.left = handleChangeToBalanceTree(root.left);
  if (!root.right) root.right = handleChangeToBalanceTree(root.right);

  const leftDeep = getDeep(root.left),
    rightDeep = getDeep(root.right);
  if (Math.abs(leftDeep - rightDeep) < 2) {
    return root;
  } else if (leftDeep > rightDeep) {
    // 左边深
    // 判断是否需要右左双旋
    const changeBranchDeep = getDeep(root.left.right);
    const noChangeBranchDeep = getDeep(root.left.left);
    if (changeBranchDeep > noChangeBranchDeep) {
      root.left = handleLeftRotate(root.left);
    }
    // 判断是否需要右右双旋
    let newRoot = handleRightRotate(root);
    newRoot.right = handleChangeToBalanceTree(newRoot.right);
    // 右子树修改后新的二叉树可能不平衡
    newRoot = handleChangeToBalanceTree(newRoot);
    return newRoot;
  } else {
    // 右边深
    // 判断是否需要左右双旋
    const changeBranchDeep = getDeep(root.right.left);
    const noChangeBranchDeep = getDeep(root.right.right);
    if (changeBranchDeep > noChangeBranchDeep) {
      root.right = handleRightRotate(root.right);
    }
    // 判断是否需要左左双旋
    let newRoot = handleLeftRotate(root);
    newRoot.left = handleChangeToBalanceTree(newRoot.left);
    // 左子树修改后新的二叉树可能不平衡
    newRoot = handleChangeToBalanceTree(newRoot);
    return newRoot;
  }
};

9.234 树

1）由来

如何让查找的效率尽可能高
- 树的层级越少，查找效率越高
如何让二叉平衡排序树的层数尽可能少
- 不是二叉，层数就会更少
- 但是叉越多，树的结构越复杂
影响二叉平衡排序树的性能的点在哪
- 二叉平衡排序树只能有两个叉，导致在节点铺满的时候也会有很多层
- 一个节点只能存一个值，空间利用率低

结论

树的搜索性能在度为 4 时最好

2）含义

新增加的节点永远在最后一层
这棵树永远是平衡的，即每一条路径高度都相同

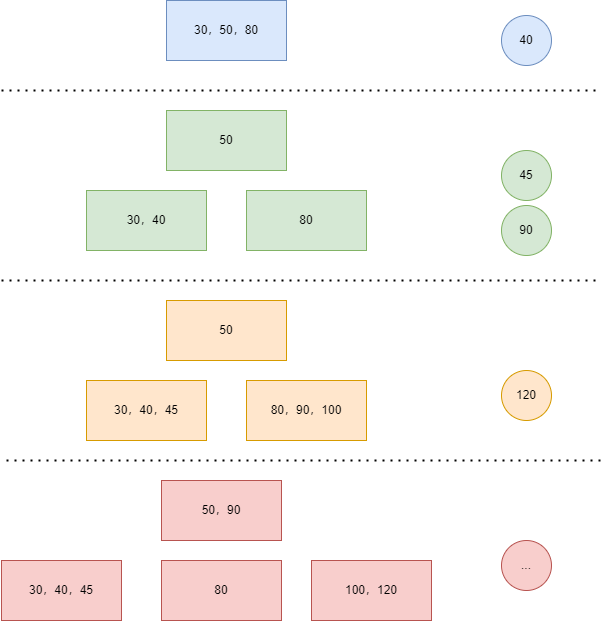
3）优点

分支变多了，层数变少了
节点中存储的数变多了，节点变少了

4）缺点

分支多了，复杂度增加了

5）期望

简化为二叉
保留多叉
单节点可以存放多个值

10.红黑树

1）性质

节点是红色或黑色
根节点是黑色
每个红色节点的两个子节点都是黑色
- 从每个叶子节点到根节点的所有路径上不能有连续两个红色节点
从任一节点到其每个叶子节点的所有路径都包含相同数目的黑色节点

2）解释

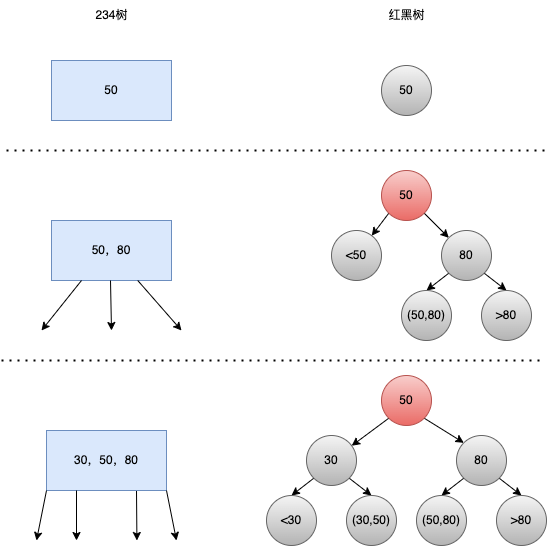
红色代表虚拟节点，黑色代表真实节点
遍历时略过红色节点，只算黑色节点
红色节点用于表示多个叉路，必须同下层黑色节点一起组合起来才有意义
- 物理上依旧是二叉树，但是红色节点在逻辑上和黑色节点形成了多叉（234 树）

11.树的深度优先搜索

一个分支走到底
再遍历下一个分支

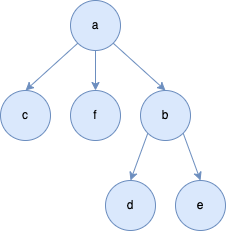
const deepSearchTree = (root, target) => {
  if (!root) return false;
  if (root.value === target) return true;
  let res = false;
  root.children.forEach((child) => (res |= deepSearchTree(child, target)));
  return !!res;
};
console.log(deepSearchTree(a, "c")); // true
console.log(deepSearchTree(a, "n")); // false

12.树的广度优先搜索

一层一层遍历
每遍历一个节点则保存当前节点的子节点
未找到则递归遍历子节点

const broadcastSearchTree = (roots, target) => {
  if (!roots || roots.length === 0) return false;
  let children = [];
  for (const root of roots) {
    if (root.value === target) return true;
    else children = [...children, ...root.children];
  }
  return broadcastSearchTree(children, target);
};
console.log(broadcastSearchTree([a], "c")); // true
console.log(broadcastSearchTree([a], "n")); // false

13.图的深度优先搜索

在树的深搜基础上，必须避免环的产生
每遍历一个节点，需要将当前遍历过的路径保存起来
判断当前节点是否遍历过是在递归入口处

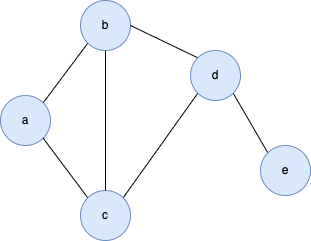
const deepSearchGraph = (node, target, searched) => {
  if (!node) return false;
  if (searched.includes(node)) return false;
  if (node.value === target) return true;
  searched.push(node);
  let res = false;
  node.neighbor.forEach((child) => (res |= deepSearchGraph(child, target, searched)));
  return !!res;
};
console.log(deepSearchGraph(a, "c", [])); // true
console.log(deepSearchGraph(a, "n", [])); // false

14.图的广度优先搜索

在树的广搜基础上，必须避免环的产生
每遍历一个节点，需要将当前遍历过的路径保存起来
判断当前节点是否遍历过是在遍历循环中，因为递归入口处的 nodes 是数组

const broadcastSearchGraph = (nodes, target, searched) => {
  if (!nodes || nodes.length === 0) return false;
  let children = [];
  for (const node of nodes) {
    if (searched.includes(node)) continue;
    searched.push(node);
    if (node.value === target) return true;
    else children = [...children, ...node.children];
  }
  return broadcastSearchGraph(children, target, searched);
};
console.log(broadcastSearchGraph([a], "c", [])); // true
console.log(broadcastSearchGraph([a], "n", [])); // false

提示

图的深搜、广搜经常用于爬虫爬取页面

（九）动态规划

只需关注每一个状态是如何得到的
下一个状态由递归求出

1.斐波那契数列

0, 1, 1, 2, 3, 5, 8, 13, 21, ...
给出 n，求第 n 位的值

1）普通算法

const fibonacci = (n) => {
  if (n <= 0) return -1;
  if (n === 1) return 0;
  if (n === 2) return 1;
  let a = 0,
    b = 1,
    c;
  for (let i = 3; i <= n; i++) {
    c = a + b;
    a = b;
    b = c;
  }
  return c;
};
console.log(fibonacci(5)); // 3

2）动态规划

f(n) = f(n - 1) + f(n - 2)

const fibonacci = (n) => {
  if (n <= 0) return -1;
  if (n === 1) return 0;
  if (n === 2) return 1;
  return fibonacci(n - 1) + fibonacci(n - 2);
};
console.log(fibonacci(5)); // 3

2.青蛙跳台阶问题

一只青蛙，一次只能跳一级台阶或两级台阶，问跳到第 n 级台阶有多少种跳法
跳到第 n 级台阶时，必定是从 n-1 级台阶或者 n-2 级台阶跳上来的
f(n) = f(n - 1) + f(n - 2)

const jump = (n) => {
  if (n <= 0) return -1;
  if (n === 1) return 1;
  if (n === 2) return 2;
  return jump(n - 1) + jump(n - 2);
};
console.log(jump(4));
/**
 * 1 1 1 1
 * 1 1 2
 * 1 2 1
 * 2 1 1
 * 2 2
 */

3.变态青蛙跳台阶问题

一只青蛙，一次能跳一级台阶或两级台阶或 n 级台阶，问跳到第 n 级台阶有多少种跳法
f(n) = f(n - 1) + f(n - 2) + f(n - 3) + ... + f(2) + f(1) + f(0)

const jump = (n) => {
  if (n <= 0) return -1;
  if (n === 1) return 1;
  if (n === 2) return 2;
  let res = 0;
  for (let i = 1; i < n; i++) {
    res += jump(n - i);
  }
  // + 1 表示从第0级台阶跳上来，即 f(0)
  return res + 1;
};
console.log(jump(4));
/**
 * 1 1 1 1
 * 1 1 2
 * 1 2 1
 * 2 1 1
 * 2 2
 * 1 3
 * 3 1
 * 4
 */

一、前端必会算法

# （一）数据结构与算法

# 1.数据结构

# 2.算法

# （二）线性数据结构

# 1.数组

# 1）特性

# 2）优点

# 3）缺点

# 4）声明

# 2.链表

# 1）特性

# 2）优点

# 3）缺点

# 4）声明

# 3.线性数据结构的遍历

# 1）循环遍历数组

# 2）循环遍历链表

# 3）递归遍历数组

# 4）递归遍历链表

# 4.链表的逆置

# 1）找到最后一个节点

# 2）找到倒数第二个节点

# （三）排序

# 1.比较

# 2.交换

# 3.冒泡排序

# 4.选择排序

# 5.简单快速排序

# 1）思想

# 2）排序

# 6.标准快速排序

# 1）思想

# 2）排序

# （四）栈和队列

# 1.栈结构

# 2.队列结构

# （五）双向链表

# 1.优点

# 2.缺点

# 3.实现

# （六）二维数据结构

# 1.二维拓扑结构（图）

# 1）拓扑

# 2）二维

# 3）实现

# 2.邻接表

# （七）树形结构

# 1.基本特点

# 2.二叉树

# 1）满二叉树

# 2）完全二叉树（国内定义）

# 3）完全二叉树（国际定义）

# 4）子树

# 3.二叉树的遍历

# 1）构造树

# 2）前序遍历

# 3）中序遍历

# 4）后序遍历

# 4.还原二叉树

# 1）根据前序中序还原二叉树

# 2）根据中序后序还原二叉树

# （八）搜索

# 1.二叉树的搜索

# 1）深度优先搜索

# 2）广度优先搜索

# 2.二叉树的比较

# 1）左右子树互换后不是同一棵树

# 2）左右子树互换后视为同一棵树

# 3.二叉树的 diff 算法

# 4.图的搜索（最小生成树问题）

# 1）目标

# 2）图的表示

# 3）算法 1：普利姆算法（加点法）

# 4）算法 2：克鲁斯卡尔算法（加边法）

# 5.二叉搜索树

# 1）经典问题

# 2）构建二叉搜索树

# 3）搜索二叉搜索树

# 6.平衡二叉树（二叉平衡搜索树）

（一）数据结构与算法

1.数据结构

2.算法

（二）线性数据结构

1.数组

1）特性

2）优点

3）缺点

4）声明

2.链表

1）特性

2）优点

3）缺点

4）声明

3.线性数据结构的遍历

1）循环遍历数组

2）循环遍历链表

3）递归遍历数组

4）递归遍历链表

4.链表的逆置

1）找到最后一个节点

2）找到倒数第二个节点

（三）排序

1.比较

2.交换

3.冒泡排序

4.选择排序

5.简单快速排序

1）思想

2）排序

6.标准快速排序

1）思想

2）排序

（四）栈和队列

1.栈结构

2.队列结构

（五）双向链表

1.优点

2.缺点

3.实现

（六）二维数据结构

1.二维拓扑结构（图）

1）拓扑

2）二维

3）实现

2.邻接表

（七）树形结构

1.基本特点

2.二叉树

1）满二叉树

2）完全二叉树（国内定义）

3）完全二叉树（国际定义）

4）子树

3.二叉树的遍历

1）构造树

2）前序遍历

3）中序遍历

4）后序遍历

4.还原二叉树

1）根据前序中序还原二叉树

2）根据中序后序还原二叉树

（八）搜索

1.二叉树的搜索

1）深度优先搜索

2）广度优先搜索

2.二叉树的比较

1）左右子树互换后不是同一棵树

2）左右子树互换后视为同一棵树

3.二叉树的 diff 算法

4.图的搜索（最小生成树问题）

1）目标

2）图的表示

3）算法 1：普利姆算法（加点法）

4）算法 2：克鲁斯卡尔算法（加边法）

5.二叉搜索树

1）经典问题

2）构建二叉搜索树

3）搜索二叉搜索树

6.平衡二叉树（二叉平衡搜索树）

7.二叉树的单旋